Recipe to deduce mod-4 cohomology from mod-2 cohomology
With a pinch of life lessons.
In the past few weeks I’ve been working on some fairly intricate computations with spectral sequences (I might write about those in the near future). A few days ago, to my despair, I reached contradicting results – meaning somewhere in my calculation there must hide an error. This is a really devastating feeling, especially after so much effort, because I had no idea where the error lies. The computation is so intricate and has so many steps; so many results depending on preceding ones.
After a day or two of wanting to give up entirely, I decided to buckle down and start anew, this time set out to carefully prove each step I make; verify each conclusion; triple-check each intermediate result. Lucky for me my mistake occured pretty early on, so it didn’t take too long to find. It also happened in a place that shouldn’t affect too many of the later steps of the computation, which means not all hope is lost.
Looking back, although it never feels good to make errors, I am actually really satisfied with how I made that error. This is for two reasons:
- Firstly, I felt very confident in all the steps of my computation, except for one – and this one particular “weak link” was also where I found my mistake. I was worried that I felt confident in understanding something that would turn out to be completely wrong, but no – my confidence was quite well-placed.
- Secondly, I got to learn a new piece of math from this whole experience. Learning from mistakes is probably the most memorable way to learn!
That second thing is what the rest of this post will discuss. But before I get to the proper math, it certainly is important to acknowledge this constant cycle of studying math, getting stuck, and feeling devastated, just to come back later and realize so clearly what went wrong. Maybe that’s a lesson for future experiences not to give up when I’m stuck. Or perhaps, even when I do give up, it’s only temporary! All it takes is some time away to clear my head and get back with a fresh perspective.
My false presumption
To explain what my misunderstanding was, let me begin with a more standard result. This is a sort of “recipe” which allows you to recover integral cohomology (with $\mathbb{Z}$ coefficients) from the knowledge of mod-$2$ cohomology (with $\mathbb{Z}/2$ coefficients). The latter is much more computable in practice, thanks to e.g. the Künneth isomorphisms & perfect duality between co/homology, which do not hold integrally without some correction terms.
But to fully recover integral cohomology you also need to know of the “higher Bocksteins”. The first Bockstein homomorphism is the usual one: you start from the short-exact sequence
\[0 \xrightarrow{\quad\quad} \mathbb{Z}/2 \xrightarrow{\quad\times 2\quad} \mathbb{Z}/4 \xrightarrow{\quad\mathrm{mod}_2\quad} \mathbb{Z}/2 \xrightarrow{\quad\quad} 0\]this induces a long-exact sequence on cohomology with corresponding coefficients1
\[\cdots \to H^{*-1}(;\mathbb{Z}/2) \xrightarrow{\beta_1} H^*(;\mathbb{Z}/2) \xrightarrow{\times2} H^*(;\mathbb{Z}/4) \xrightarrow{\mathrm{mod}_2} H^*(;\mathbb{Z}/2) \xrightarrow{\beta_1} H^{*+1}(;\mathbb{Z}/2) \to \cdots\]The (first) Bockstein is the connecting homomorphism $\beta_1$ in this sequence. It has a few nice properties, such as being a differential:
\[\beta_1\circ\beta_1 = 0\]and a graded-derivation (bars $||$ denotes the degree of a cohomology class):
\[\beta_1(x\cdot y) = \beta_1(x)\cdot y + (-1)^{|x|}x\cdot\beta_1(y)\]The higher Bocksteins are defined similarly, as connecting homomorphisms of more general short-exact sequences of coefficients:
\[0 \to \mathbb{Z}/2^k \xrightarrow{\times 2} \mathbb{Z}/2^{k+1} \xrightarrow{\mathrm{mod}_{2^k}} \mathbb{Z}/2^k \to 0 \qquad\rightsquigarrow\qquad \beta_k : H^*(;\mathbb{Z}/2^k) \to H^{*+1}(;\mathbb{Z}/2^k)\]More generally you can replace the base $2$ by any other number (typically a prime).
As you can see from the long-exact sequence, $\beta_k$ measures the “failure of liftability”. That is, if $x$ is a cohomology class with coefficients $\mathbb{Z}/2^k$, then it lifts to coefficients $\mathbb{Z}/2^{k+1}$ if and only if it’s in the image of the reduction map $\mathrm{mod}_{2^k}$, if and only if it’s in the kernel of $\beta_k$. If you class is indeed in the kernel of $\beta_k$ then you can choose a (not necessarily unique) lift to coefficients $\mathbb{Z}/2^{k+1}$, and then check if it’s in the kernel of the next Bockstein $\beta_{k+1}$. This provides an inductive procedure to determine how far up the mod-$2$ classes can be lifted, with the limit being integral cohomology2.
By following this idea even further, you can in fact construct a Bockstein spectral sequence (BSS), whose starting page is the mod-$2$ cohomology, and the differentials in the $k$th page are precisely $\beta_k$ 3. This is fairly high-brow, but the BSS actually has a very concrete practical implication: it gives you a “recipe” for recovering integral cohomology from mod-$2$ cohomology.
Recipe (from $\mathbb{Z}/2$ to $\mathbb{Z}$):
- Every pair of nonzero elements $x\in H^{n-1}(;\mathbb{Z}/2)$ and $y \in H^n(;\mathbb{Z}/2)$, connected by the $k$th Bockstein $x \xmapsto{\beta_k} y$, contributes one copy of $\mathbb{Z}/2^k$ inside $H^n(;\mathbb{Z})$.
- Every nonzero element $z \in H^n(;\mathbb{Z}/2)$ such that $z \xmapsto{\beta_k} 0$ for all $k$, and such that $z$ is not in the image of any $\beta_k$ (so it’s not part of any pair, as in the first case), contributes one copy of $\mathbb{Z}$ inside $H^n(;\mathbb{Z})$.
Moreover, everything in $H^*(;\mathbb{Z})$ arises this way.
This “recipe” is fairly standard, so I won’t go through its proof here.
Remark: The recipe really gives you a feel for what happens inside the BSS: the elements $z$ as in the second case are precisely those which represent something nontrivial in the “cohomology” $\frac{\ker\beta_k}{\operatorname{im}\beta_k}$, and this is precisely how you “turn the page” in the spectral sequence. This is quite an interesting phenomenon, because we don’t extract information from the initial page of the sequence, nor from the limiting page, but rather from the behavior of the intermediate pages that occur during the computation!
My mistake, that I mentioned in the introduction, stemmed from trynig to extrapolate from this recipe a slightly different one: how to recover mod-$4$ cohomology from mod-$2$ cohomology? Namely, I falsely assumed that a “pair” as in the first case of the above, connected by $\beta_1$, should just contribute one copy of $\mathbb{Z}/2$ in $H^n(;\mathbb{Z}/4)$.
While this is true, it’s not everything: such pair will also contribute another copy of $\mathbb{Z}/2$ in the cohomology $H^{n-1}(;\mathbb{Z}/4)$ of one lower degree. This extra copy is what caused all my woes.
The correct generalization
Now I can state my corrected recipe:
Recpie (from $\mathbb{Z}/2$ to $\mathbb{Z}/4$):
- Every pair of nonzero elements $x \in H^{n-1}(;\mathbb{Z}/2)$ and $y \in H^n(;\mathbb{Z}/2)$, connected by the first Bockstein $x \xmapsto{\beta_1} y$, contributes a copy of $\mathbb{Z}/2$ inside $H^{n-1}(;\mathbb{Z}/4)$ and another copy of $\mathbb{Z}/2$ inside $H^n(;\mathbb{Z}/4)$.
- Every nonzero element $z \in H^n(;\mathbb{Z}/2)$ such that $z \xmapsto{\beta_1} 0$, and such that $z$ is not itself in the image of $\beta_1$, contributes one copy of $\mathbb{Z}/4$ inside $H^n(;\mathbb{Z}/4)$.
Moreover, everything in $H^*(;\mathbb{Z}/4)$ arises this way.
Proving this is a nice easy exercise in diagram chasing, so I’ll briefly go through it below. It’s also a good indication for how the “original” recipe may be proved.
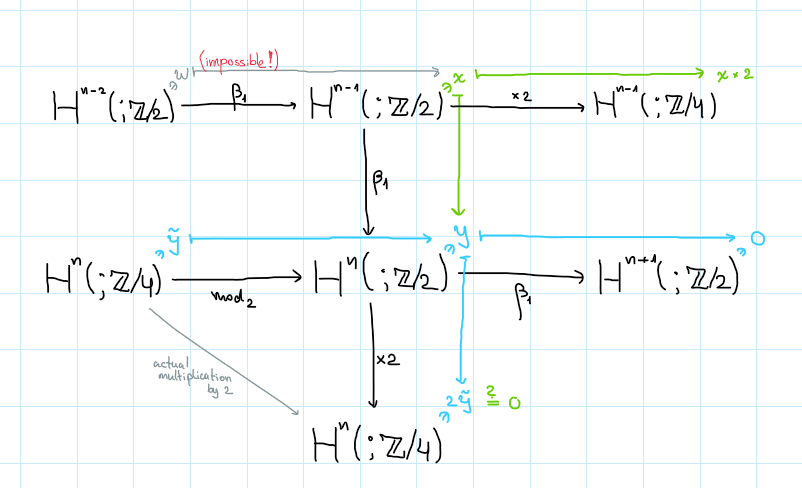
Proof of recipe: In the notation of the recipe, both $y$ and $z$ are elements lying in the kernel of $\beta_1$. The only difference between them is “why” are they in the kernel: since $\beta_1$ is a differential, anything in its image must be in the kernel – this is what causes $y = \beta_1(x)$ to land in the kernel. On the other hand, the kernel may contain elements which are not the image of anything – that’s our $z$. These ones are “caused” by nontriviality of the cohomology of the differential $\beta_1$ (so-called “Bockstein cohomology”) or more generally nontriviality of later terms in the BSS.
But anyways, let’s consider some arbitrary $y \in H^n(;\mathbb{Z}/2)$ such that $\beta_1(y) = 0$. From the long-exact sequence this means $y$ can be lifted to mod-$4$ cohomology, i.e. we can choose (not necessarily uniquely) a class $\tilde y \in H^n(;\mathbb{Z}/4)$ such that $\mathrm{mod}_2(\tilde y) = y$. If we assume $y$ is nonzero, then $\tilde y$ is also necessarily nonzero. But keep in mind, $\tilde y$ lives inside a $\mathbb{Z}/4$-module, so it can have order either $2$ or $4$, i.e. either $2\tilde y = 0$ or $2\tilde y \neq 0$, but in any case $4\tilde y = 0$.
Now there’s a subtlety: given a congruence class $y$ modulo $2$, its double $2y$ is well-defined modulo $4$ – this is where our morphism $\mathbb{Z}/2 \xrightarrow{\times 2}\mathbb{Z}/4$ comes from. However when you look at the morphism induced by this in cohomology, it cannot be naïvely interpreted as just multiplication by $2$!! For instance, even if both $H^n(;\mathbb{Z}/2)$ and $H^n(;\mathbb{Z}/4)$ happen to be isomorphic to $\mathbb{Z}/2$, then it might seem like $\mathbb{Z}/2 \xrightarrow{\times 2} \mathbb{Z}/2$ should be the zero map, but that’s not necessarily the case. The reason is, conceptually, that it might actually look like $\mathbb{Z}/2\mathbb{Z} \to 2\mathbb{Z}/4\mathbb{Z}$ – the target group is still isomorphic to $\mathbb{Z}/2$, but under this identification the map $\times 2$ would act like the identity. A similar warning applies to the reduction homomorphism $\mathrm{red}_2$: its action on cohomology may be the one you’d expect naïvely, but it may also be the zero map (as in $2\mathbb{Z}/4\mathbb{Z} \xrightarrow{\mathrm{mod}_2} \mathbb{Z}/2\mathbb{Z}$).
Despite these warnings, if you compose the two maps $\mathbb{Z}/4 \xrightarrow{\mathrm{mod}_2} \mathbb{Z}/2 \xrightarrow{\times 2} \mathbb{Z}/4$, then the induced map on cohomology actually does behave as expected in the naïve sense – it is actual multiplication by $2$ on the given $\mathbb{Z}/4$-modules. Therefore if we multiply our $y$ by $2$ we get:
\[y\times 2 = \mathrm{red}_2(\tilde y) \times 2 = 2\tilde y\]As we recalled in the first paragraph, the zero-ness/nonzero-ness of $2\tilde y$ corresponds to whether $\tilde y$ has order $2$ or order $4$. But now we also see that these precisely correspond to the two cases of our recipe:
- if $2\tilde y = 0$ then $y\times 2 = 0$, which by the long-exact sequence means $y = \beta_1(x)$ for some $x$.
- if $2\tilde y \neq 0$ then necessarily $y$ is not the Bockstein of anything. In our recipe, this $y$ would be called $z$.
Now from these two cases we can read off the contributions to mod-$4$ cohomology:
- Starting from the second case, if $2\tilde y \neq 0$ this means $\tilde y$ has order $4$, i.e. it generates a copy of $\mathbb{Z}/4$ in $H^n(;\mathbb{Z}/4)$ just as our recipe predicts.
- In the first case, it is clear that $\tilde y$ generates a copy of $\mathbb{Z}/2$ inside $H^n(;\mathbb{Z}/4)$… but our recipe predicts more than that (exactly what I missed in my own computations). In this case we also have some other $x \in H^{n-1}(;\mathbb{Z}/2)$ such that $\beta_1(x) = y$. I claim that $x\times 2 \in H^{n-1}(;\mathbb{Z}/4)$ has order exactly $2$, and thus generates another copy of $\mathbb{Z}/2$. Indeed it cannot have order $4$, because
It also cannot have order $0$, because that’d mean $x\times 2 = 0$, so by the long-exact sequence $x$ itself is the image of some $w \in H^{n-2}(;\mathbb{Z}/2)$ under the Bockstein, i.e.
\[x = \beta_1(w) \qquad\rightsquigarrow\qquad y = \beta_1(x) = \beta_1(\beta_1(w)) = 0\]which contradicts $y$ being nonzero. $\square$
Finally, here’s a cute sketch of the entire chasing argument (these are three copies of the long-exact sequence interlaced orthogonally with each other).
Footnotes
-
All cohomology groups throughout this post are of the same space, just with different coefficients. In an attempt to keep things a bit cleaner I entirely drop the space from my notation. You can actually define Bocksteins much more generally for arbitrary chain complexes. ↩
-
This of course only recovers the $2$-primary part, as a module over $\mathbb{Z}[2^\infty]$; to get full integral knowledge you must perform the same procedure at all other primes. ↩
-
Technically, the differentials on the $k$th page should be $\beta_{k-1}$, because the “initial page” of the spectral sequence starts in page $2$. Also, the objects in the later pages do not directly appear as cohomology with $\mathbb{Z}/2^k$ coefficients, so this only makes sense up to an appropriate isomorphism. ↩